Esta é uma questão de topologia. Existem três tentativas principais de ordenar fluxos de pequenos a maiores.

O primeiro foi estabelecido por Horton (1941) que estabeleceu o conceito de composição da drenagem . Para estabelecer a importância relativa dos córregos em uma rede, Horton sugeriu investigar cada junção e definir o fluxo que entrou na junção no ângulo mais alto como um fluxo de menor importância. Ao começar na foz de um rio, pode-se estabelecer qual seria o tronco principal de um rio e quais são os afluentes cada vez menores. O número de pedido dos fluxos não pode ser determinado até que toda a árvore de fluxos tenha sido ordenada. Na figura na ordem do riacho de Strahler, a diagonal seria o tronco principal do rio e teria ordem três. O único tronco de ordem dois seria aquele rotulado como dois voltando para baixo de três na figura.

Strahler, 1952 levou o conceito adiante e estabeleceu o conceito de ordem do fluxo . Nesta abordagem, o fluxo básico é o menor afluente de origem. Quando dois fluxos de ordem um se encontram, eles formam um fluxo de ordem dois. São necessários dois da mesma ordem para fazer um fluxo de ordem maior, de modo que um fluxo de ordem dois e um não aumentará o número do pedido, o resultado ainda é dois. A imagem a seguir fornece um exemplo da ordem do fluxo de Strahler:

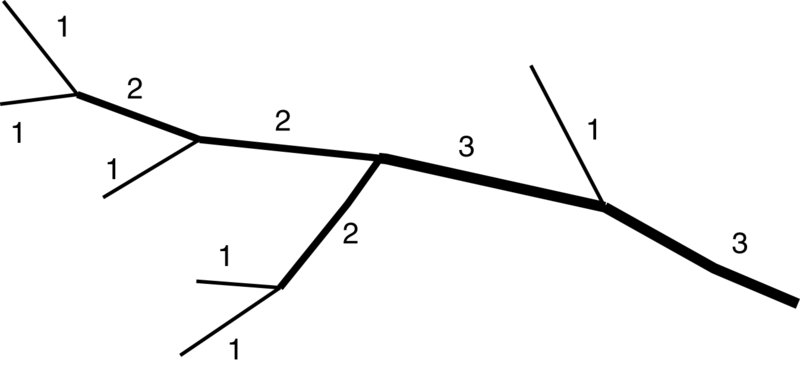
Conceito de ordem do fluxo de Strahler. Imagem da Wikipédia comum

A ordem do fluxo permite calcular um conjunto de medidas estatísticas que caracterizam uma bacia de drenagem e é possível usar essas características, por exemplo, na previsão de enchentes.

Shreve (1967) levou as idéias de Horton e Strahler mais longe ao introduzir magnitude, agora chamada de Magnitude de Shreve . Este conceito difere do de Strahler porque todos os riachos são aditivos, de modo que, assim que um riacho é adicionado a outro, o riacho resultante é a soma dos dois afluentes. O resultado é que o sistema pode ser visto como refletindo a descarga, assumindo que todos os fluxos de primeira ordem são de tamanho semelhante. Na figura acima, a maior magnitude seria seis, esta também é a soma de todos os córregos de ordem um.

Portanto, estabelecer o tronco principal de um rio não é necessariamente simples. O método de Hortons faz isso, mas ao mesmo tempo depende da geometria e os rios podem ser fortemente influenciados pela geologia para gerar padrões estranhos de rios.

Referências :

Horton, RE, 1945. Desenvolvimento erosional de córregos e suas bacias de drenagem: abordagem hidrofísica da morfologia quantitativa. Boletim da Sociedade Geológica da América , 56, 275-370. doi: 10.1130 / 0016-7606 (1945) 56 [275: EDOSAT] 2.0.CO; 2

Shreve, R.L., 1967. Redes de canais topologicamente aleatórios infinitos. Journal of Geology 75, 178–186.

Strahler, A.N., 1952. Hypsometric (area-altitude) analysis of erosional topology. Geological Society of America Bulletin , 63 (11), 1117–1142, doi: 10.1130 / 0016-7606 (1952) 63 [1117: HAAOET] 2.0.CO; 2.